El Problema de Calendarizar las Máquinas en un Taller de Manufactura
Job Shop Scheduling
El problema que se pretende resolver es el de encontrar la mejor secuencia de operaciones dentro de un conjunto de máquinas para la realización de un conjunto de trabajos, que minimice el Makespan. El Makespan es el tiempo de terminación del último trabajo.
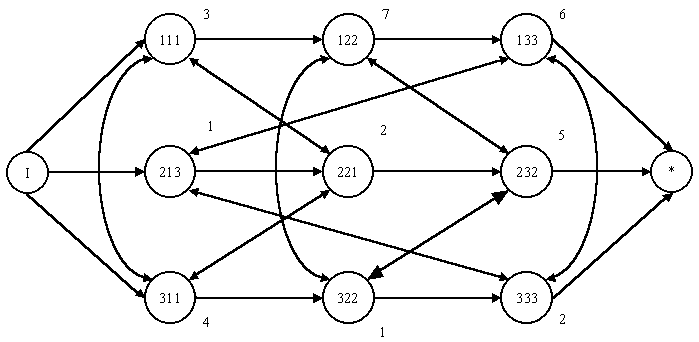
Representación de JSSP con un grafo disyuntivo.
Generalmente JSSP (Job Shop Scheduling Problem) se representa en forma de un grafo disyuntivo G = (O, C, D) el cual consiste de lo siguiente: Un conjunto de operaciones O etiquetadas cada una como (i, j, k), donde i es el número de trabajo en el sistema, j es el número de operación (nodo en el grafo) que se ejecuta dentro del trabajo i, y k es el número de máquina donde se ejecuta la operación j del trabajo i. Se tiene un conjunto C de arcos conjuntivos que forman subconjuntos, cada uno de estos subconjuntos representan a cada trabajo, por ejemplo en la figura 1, las operaciones (111),(122) y (133) que representan al trabajo 1 están unidas por un subconjunto de arcos conjuntivos. Se tiene un conjunto de arcos D disyuntivos, también llamados arcos no dirigidos. Estos arcos forman subconjuntos de cliques, que representan a una máquina cada uno. En el grafo de la figura 1, se puede ver que para resolver el problema, se requiere de encontrar la mejor secuencia en cada máquina que permita fijar los arcos disyuntivos en arcos dirigidos, evitando ciclos locales y globales, con el fin de minimizar el Makespan. De esta forma, una vez encontrada la mejor secuencia de operaciones en cada máquina, lo único que resta es hacer la calendarización (Scheduling) de las operaciones de acuerdo a la secuencia obtenida.

Figura 1. JSSP de tres trabajos y tres máquinas.
La calendarización del problema se esquematiza a través del diagrama de Gantt. El demo 1, presenta diversas soluciones (todas óptimos globales) para el JSSP Benchmark de Muth y Thompson [1] de 10x10, obtenidas por un algoritmo propuesto de Recocido Simulado con cooperación de procesos. Los primeros que encontraron la solución óptima a este Benckmark fueron Carlier y Pinzon [2] utilizando su algoritmo de ramificación y acotamiento. Esta solución se encontró 20 años después de haber sido propuesto el Benchmark. El eje x, corresponde a las unidades de tiempo en las que se inicia y termina la ejecución de cada una de las operaciones de los trabajos, y el eje y, corresponde a las máquinas presentes en el sistema.
Demo 1. Diagrama de Gantt de la solución óptima del benchmark de Muth y Thompson del JSSP de 10x10 que da la secuencia de trabajos por máquina mostrando su calendarización.
La Figura 2, presenta una aproximación al mejor solución conocida para el JSSP Benchmark YN2 de Nakano y Yamada de 20x20, obtenida por un algoritmo propuesto de Recocido Simulado con cooperación de procesos implementando un algoritmo de aproximación a la ruta critica [3] para la función de vecindad. El tiempo para obtener esta solución aproximada fue de 3 hrs., con 10 minutos. Con un error relativo de 0.33% con respecto al mejor conocido. El eje x, corresponde a las unidades de tiempo en las que se inicia y termina la ejecución de cada una de las operaciones de los trabajos, y el eje y, corresponde a las máquinas presentes en el sistema.

Figura 2. Diagrama de Gantt de una solución aproximada (MS = 912) a la mejor conocida (MS = 909) del benchmark YN2 de Nakano y Yamada del JSSP de 20x20 que da la secuencia de trabajos por máquina mostrando su calendarización.
En el JSSP, una de las funciones objetivo que se busca minimizar es la de reducir el tiempo de termino del último trabajo (Makespan). Generalmente en las meta heurísticas utilizadas para minimizar el Makespan, como Algoritmos Meméticos, Recocido Simulado y otros tipos de búsquedas locales iteradas, se utiliza la función de vecindad del tipo N1, la cual ha dado buenos resultados cuando se restringe la permutación de pares de operaciones a pares que pertenecen a la Ruta Crítica del JSSP [3]. En la siguiente liga se presenta una explicación del método CPM para encontrar la Ruta Critica en un JSSP:
CPM in The Job Shop Scheduling Problem
1.- J. F. Muth and G. L. Thompson, Industrial Scheduling, Prentice Hall, Englewood Cliffs, New Jersey, Ch 15, pp. 225-251, 1963.
2.- J. Carlier and E. Pinson, An algorithm for solving the job-shop problem. Manage. Sci., 35(2): 164-176, 1989.
3.- P.J.M. Van Laarhoven, E.H.L. Aarts and J.K. Lenstra. Job shop scheduling by simulated annealing. Oper. Res., 40(1):113-125, 1992.
4.- M. A. Cruz-Chávez, J. Frausto-Solís, A New Algorithm that Obtains an Approximation of the Critical Path in the Job Shop Scheduling Problem, Lecture Notes in Artificial Intelligence, Springer Verlag Pub., Berlin Heidelberg, ISSN: 0302-9743, Vol.4293, pp.450-460, 2006.